フラクション。普通、小数、混合の端数の乗算

中高生の場合「分数」のテーマを通過しました。しかし、このコンセプトは、学習プロセスで与えられたよりもはるかに広いです。今日、分数の概念は非常に頻繁に発生し、すべての式を計算することはできません。たとえば、分数を掛けるなどです。

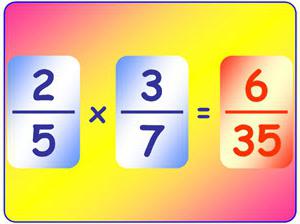
端数とは何ですか？

歴史的に、分数測定の必要性のために登場した。実践が示すように、セグメントの長さ、直方体の体積、長方形の面積を決定する例がしばしばある。

当初、学生はそのようなコンセプト、シェアたとえば、スイカを8つの部分に分割すると、それぞれが8つのスイカを取得します。この8つの部分の1つをシェアと呼びます。

任意の値の1/2に等しいシェアを半分と呼びます。 1/3 - 第3; 1/4 - 四半期。フォームの記録 ⁵/₈, ⁴/₅, ²/₄ 通常の分数と呼ばれます。 普通分数は分子と分母に分かれています。それらの間には、小数点の特徴、または小数点の行があります。分数線は、水平線または傾斜線として描くことができます。ここでは、除算記号を示します。

分母は、数量がオブジェクトによって分割された数を表します。分子 - 何本の同一の株式が取られるか。分子は分数線の上に書かれ、その下に分母が書かれる。

通常の分数を表示するのが最も便利です座標線。 1つのセグメントを4等分した場合は、各シェアをラテン文字で指定すると、優れた視覚効果を得ることができます。したがって、点Aは、 ¹/₄ 単位区間全体から、点Bのマーク ²/₈ このセグメントの

フラクションの変動

分数は通常、小数、および混合数です。さらに、分数は規則的および不規則に分けることができる。この分類は、通常の分数に適しています。

正しい小数は、分子は分母より小さい。従って、不規則部分は、分子が分母よりも大きい数である。第2の種類は通常、混在した数字の形で書かれています。この式は、整数部分と小数部分で構成されます。たとえば、1/2です。 1 - 整数部分、1/2分数。しかし、式を使っていくつかの操作（分数の除算や逓倍、縮小、変換）を行う必要がある場合、混合数は正しくない部分に変換されます。

正しい分数式は常に1より小さく、間違った分数式は1以上です。

小数は、この表現とは、任意の数が表現されたレコードを意味し、その分数表現の分母は、いくつかのゼロを有する単位として表現することができる。端数が正しい場合、小数点表記の整数部分はゼロになります。

小数を記録するには、最初に部分全体を書き、小数部からカンマで区切り、分数式を書いてください。コンマの後、分子は分母のゼロと同数の数字を含んでいなければならないことに注意してください。

例：。 7の一部を提示する²¹/₁₀₀₀ 10進表記で表します。

不規則な分数を混合数に変換するアルゴリズムとその逆の変換

問題の答えに間違った部分を記録するのは間違っているため、混合番号に変換する必要があります。

• 分子を既存の分母で除算する。
• 特定の例では、不完全な商は整数である。
• 残りは小数部分の分子であり、分母は変更されません。

例：。間違った部分を混合した数に変換する： ⁴⁷/₅.

ソリューション。 47：5である。不完全な商は9に等しく、余りは2である。したがって、 ⁴⁷/₅ = 9²/₅.

混乱した数を不規則な部分として表示する必要があることがあります。次に、次のアルゴリズムを使用する必要があります。

• 部分全体が部分式の分母によって乗算される。
• 得られた生成物は分子に加えられる。
• 結果は分子に書かれ、分母は変わらない。

例：。混合した形で数を不規則な小数部として表現する：9⁸/₁₀.

ソリューション。 9×10 + 8 = 90 + 8 = 98が分子です。

返信： ⁹⁸/_10.

普通の分数の掛け算

一般的な分数を超えることができます異なる代数演算。 2つの数値を乗算するには、分子と分母と分母と分子を乗算する必要があります。また、異なる分母を有する画分の乗算 同じ分母を持つ分数の積と異ならない。

あなたが必要とする結果を見つけたら分数を切り取る。結果として得られる表現を可能な限り単純化することが絶対に必要です。もちろん、答えの間違った部分は間違いだとは言えませんが、正しい答えを呼び出すことも難しいです。

例：。 2つの通常の分数の積を求める：½と ²⁰/₁₈.

実施例からわかるように、生成物を見出した後、還元可能な分数記録が得られた。この場合の分子と分母の両方を4で除算し、その結果を答え ⁵/₉.

小数点の掛け算

小数部分の積は、それ自体の方法で普通のものの積からかなり異なっています。したがって、分数の乗算は次のようになります。

• 小数点以下2桁は、右下の数字がもう一方の下になるように下位に書き込まなければなりません。
• カンマにもかかわらず、自然数として記録された数を掛けることが必要です。
• 各数字の小数点以下の桁数を計算します。
• 結果を乗算した後の結果では、コンマの後に両方の要素の合計にある数の数字を数え上げて区切り記号を付ける必要があります。
• 製品内の数字が小さい場合は、数字の前にカンマを入れて全体を0に設定する必要があります。

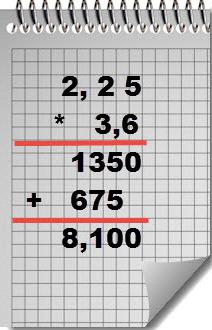
例：。小数点以下2桁の積：2.25と3.6を計算します。

ソリューション.

混合分数の乗算

2つの混合分の積を計算するには、乗算ルールを使用する必要があります。

• 混在した数を不規則な分数に変換する。
• 分子の積を求める。
• 分母の積を求める。
• 結果を記録する。
• 可能な限り表現を簡素化する。

例：。製品を探す4 1と6²/_5.

数を分数で掛ける（数を端数で割る）

2つの分数（混合数）の積を求めることに加えて、自然数に分数を掛ける必要がある仕事があります。

したがって、小数と自然数の積を求めるには、次のものが必要です。

• 分数の下に数字を書き、右端の数字が上下になるようにします。
• コンマにもかかわらず、製品を見つける。
• 小数点以下の桁数を数えて小数点以下をカンマで区切ります。

通常の分数に数を掛けるには、分子と自然因数の積を求める必要があります。回答が還元可能な割合であれば、それは変換されるべきです。

例：。製品を計算する ⁵/₈ 12。

ソリューション. ⁵/₈ * 12 = ^（5×12）/₈ = ⁶⁰/₈ = ³⁰/₄ = ¹⁵/₂ = 7¹/_2.

返信：7¹/_2.

前の例からわかるように、結果を短くし、間違った分数式を混合数に変換する必要がありました。

分数の乗算はまた、混合された形態の数と自然因子との積である。これらの2つの数を乗算するには、混合係数の全部に数を掛け、分子に同じ値を掛け、分母を変更しないでください。必要に応じて、結果を可能な限り簡素化する必要があります。

例：。製品を探す9⁵/₆ 9。

ソリューション. 9⁵/₆ x 9 = 9×9 + ^（5×9）/₆ = 81 + ⁴⁵/₆ = 81 + 7³/₆ = 88¹/_2.

返信：88¹/_2.

10,100,1000または0.1の因子による乗算; 0.01; 0,001

上記のルールは以下を意味します。 小数部を10,100,1000,10000などで乗算するには、乗数の後にゼロがあるように、数字の桁数だけ右にカンマを移動します。

例1。 0.065と1000の積を求める。

ソリューション。 0.065×1000 = 0065 = 65。

返信65。

例2。製品3.9と1000を検索します。

ソリューション。 3.9×1000 = 3.900×1000 = 3900。

返信3900。

自然数と0,1を掛ける必要がある場合、0.01; 0.001; 0.0001などの場合は、ゼロの数が最大1になるように数字の桁数だけ、結果の作業のカンマを左に移動する必要があります。必要に応じて、自然数の前に十分な量のゼロが書き込まれます。

例1。 56と0.01の積を求める。

ソリューション。 56×0.01 = 0056 = 0.56。

返信：0.56。

例2。製品4と0,001を探します。

ソリューション。 4×0.001 = 0004 = 0.004。

返信0.004。

したがって、異なる分数の積を求めることは、結果の計算を除いて、困難を生じさせてはならない。この場合、電卓なしではできません。