逆行列の実際の応用と発見

マトリックスは、特定の順序で数字の特定のセット。この用語は、著名な英国の理論理論家であるJames Sylvesterによって流布されました。彼はこれらの数学的要素を適用する理論の創始者の一人である。

今日まで、彼らは広い適用を見出している人間活動の様々な枝で逆行列を見つけるなどの方法に基づいて構築された様々な計算を実行するときに、この方法は、様々な方程式の系の未知パラメータの決定に基づいており、経済計算の実施によく使用されます。

データには次のような特殊なケースがあります数学的要素：小文字、列、ゼロ、正方形、対角、単一。小文字は要素の1行だけで構成され、列1は1列の数字で構成されます。ゼロ - すべての要素は0に等しい。そのような数学的要素の四角形では、列の数は行の数に等しい。次に、主対角線上に位置する対角線要素では「0」と異なり、残りは「0」に等しくなければならない。単一 - これは対角行列の亜種の1つです。彼女は主対角線に「1」しかありません。

行列の例：

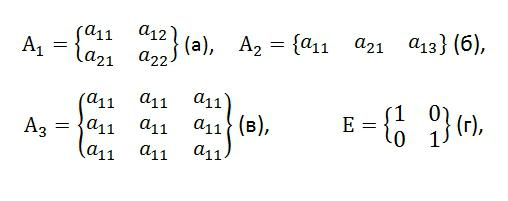
ここで：A_k総称用語である_ij - 要素、

（a）-2次;

（b） - 小文字。

（c）-3次;

（r）は2次の単位テーブルの一例である。

また、逆行列があり、その定義以下のとおりです。元の逆テーブルを掛け合わせると、単一のものが得られる。逆行列の発見を保証する多くの方法が開発されている。最も単純なものは、代数的補数と行列式の定義に基づいています（行列式とも呼ばれます）。

行列の行列式は、a₁₁a₂₂-a₁₂a_21,|А|と表記される。上記の式は、2次に対応する表に対して有効です。より高次の行列の行列式の式があります。行列式が存在するための必須の条件は、表が正方形でなければならないということです。実際には、この理論のこの要素は、逆行列を見つけるような手順で最も頻繁に使用されます。

要素の値を見つけるための第2の重要な要素は、代数的補数です。次の式で計算されます。A_ij=（-1） ^私は⁺^j* M_ijここで、Mはマイナーです。本質的に、これは、要素が位置する行と列を精神的に削除することによって得ることができる追加の決定要因である。例えば、テキスト中で先に与えられた2次に対応する表の場合、要素a₁₁ 代数的補数は、要素a₂₂.

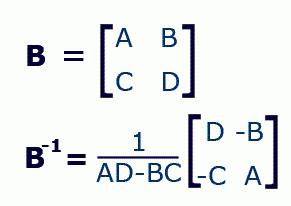
逆行列は3段階で求められる。第一段階は、決定基を定義します。全ての補助因子、そのインデックスに応じて記録され、それは表補因子が判明している - 次のステップで。行列式の各代数加算を乗算終了知見により得られた逆行列の最終段階で。