重要なポイントのキネマティクス：基本概念、要素

今日の記事のテーマは、キネマティクスです重要なポイント。これは何ですか？どの概念が含まれており、この用語を与えるのにどのような定義が必要ですか？今日、これらの問題や他の多くの質問に答えようとします。

定義と概念

重要なポイントのキネマティクスは「力学」と呼ばれる物理学のサブセクションに過ぎない。彼女は、順番に、特定の身体の動きのパターンを研究します。重要なポイントのキネマティクスもこのタスクを扱いますが、一般的な方法でこれを行うわけではありません。実際、このサブセクションでは、身体の動きを記述するための方法を研究しています。この場合、いわゆる理想体だけが調査に適している。これには、物質点、絶対的なソリッドボディ、理想気体が含まれます。概念をより詳細に検討してください。私たちは皆、学校のベンチから、物質的な点は、この状況やその状況で無視できる次元の身体であることを知っています。ところで、物質点の並進運動の運動学は、物理学の第7種の教科書に最初に現れます。これは最も簡単な支店であるため、科学的な助けを借りて科学を知り始めるのが最も便利です。別の問題は、マテリアルポイントのキネマティクスの要素が何であるかです。条件付きでは、いくつかのレベルに分かれていて、理解の複雑さが異なります。たとえば、半径ベクトルについて話すと、原則としてその定義には特別な複雑さはありません。しかし、中学校や高校の学生よりも、学生がそれを理解するのがはるかに容易であることに同意するでしょう。正直言って、この言葉の特徴を高校生に説明する必要はありません。

キネマティクスの創造の歴史

何年も前、偉大な科学者アリストテレスは自由時間の獅子の分担を別の科学として物理学の研究と記述に捧げた。特に、彼は主力論と概念を提示しようとするキネマティクスにも取り組み、実用的で普通の仕事でも解決しようとしました。 Aristotleは、物質点の運動学の要素が何であるかという初期の考えを示した。彼の作品や作品はすべての人類にとって非常に貴重です。それにもかかわらず、彼の結論では、かなりの数の間違いを犯しました。それは、ある種の誤りと誤算によるものでした。アリストテレスの研究は、一度に別の科学者、ガリレオ・ガリレイに興味がありました。 Aristotleによって提唱された基本的な論文の1つは、身体の動きは強度と方向によって決定される何らかの力に作用する場合にのみ起こるということでした。ガリレオはこれが間違いであることを証明しました。力は速度パラメータに影響しますが、それ以上は影響しません。イタリア人は、力は加速の原因であることを示しており、力はそれとの相互関係においてのみ生じ得る。また、ガリレオ・ガリレオは、対応するパターンを推測して、自由落下のプロセスの研究にかなりの注意を払った。多分誰もがピサの塔に費やした彼の有名な実験について覚えているでしょう。彼の作品では、物理学者のアンペールが運動学的解の基礎を使っていました。

初期のコンセプト

先に論じたように、キネマティクスは方法を研究する理想化されたオブジェクトの動きの記述。この場合、実際には、数学的解析、通常の代数、幾何学の基礎を適用することができます。しかし、このサブセクションの基礎となる概念（コンセプト、定義およびパラメトリック値）は何ですか？まず、力点を考慮せずに、マテリアルポイントの並進移動のキネマティックスがムーブメントを考慮することを誰もが明確に理解しなければなりません。つまり、対応する問題を解くために、力に関連する公式は必要ありません。どれくらいの数（1、2、3、少なくとも数十万）に関わらず、キネマティクスは考慮されていません。それにもかかわらず、加速の存在は依然として提供されている。多くの問題点において、物質点の運動の運動学は、加速度の大きさの決定を指示する。しかしながら、この現象の理由（すなわち、力とその性質）は考慮されず省略されている。

分類

我々は、運動学が探求し、適用することを発見した体に作用する力に関係なく体の動きを記述する方法。ちなみに、この作業はもうダイナミクスと呼ばれる別のサブセクションのメカニックによって処理されています。ニュートンの法則は既にそこに適用されており、少数の既知の初期データを用いて、実際には多くのパラメータを決定することができる。重要なポイントのキネマティクスの基本的な概念は、空間と時間です。そして、一般的な科学の発展やこの分野では、このような組み合わせを用いることの妥当性について疑問が生じました。

最初から古典的なものがありましたキネマティクス。それに特有の時間的および空間的な隙間の存在だけでなく、これまたはその参照枠の選択からの独立性もそうであると言える。ところで、これについては後で話します。今、何が危機にあるのかを説明してください。この場合のスペース間隔はセグメントとみなされ、時間間隔は時間間隔です。すべてが明確でなければならないようです。したがって、これらの間隔は、古典的な運動学において不変であり、言い換えれば、ある基準フレームから別の基準フレームへの遷移に依存しない絶対的であると考えられる。相対論的キネマティクスかどうか。その中で、参照フレーム間の遷移におけるギャップは変化し得る。おそらく彼らはそうすることはできないが、そうすべきであると言うことは正しいだろう。このため、2つのランダムな事象の同時性も相対的なものとなり、特別な配慮が必要となる。だから、相対主義的な運動学では、空間と時間の2つの概念が結合されて1つになるのです。

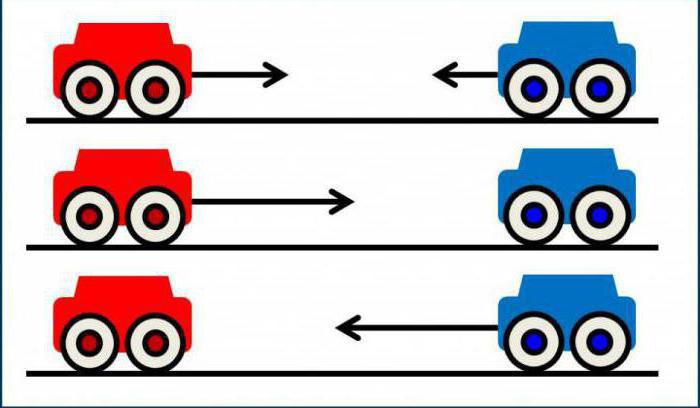
物質点の運動学：速度、加速度、およびその他の量

このセクションを少なくとも少し理解するために物理学では、最も基本的な概念を導き、定義を知り、特定の量が一般的にどのようなものであるかを表現する必要があります。これでは何も複雑ではありません。実際、すべてがとても簡単で簡単です。キネマティックスの問題で使用される基本概念を最初に考えてみましょう。

動き

機械的な動きをプロセスと見なし、その間に、1つまたは別の理想化されたオブジェクトが空間内のその位置を変える。同時に、その変化は他の身体との相対的なものであると言えるでしょう。同時に、2つのイベントの間に一定の時間間隔が存在するという事実も考慮する必要がある。たとえば、特定の間隔を選択することができます。間隔は、身体がどの位置からどのように来るかの経過時間の間に形成されます。私たちはまた、身体は機械の一般法則にしたがって互いと相互作用することができ、相互作用することに気付く。これはまさに物質的なポイントの運動学が最も頻繁に働くものです。参照フレームは、それと密接に関連している以下の概念である。

座標

通常のデータと呼ぶことができます。身体の位置を決めることができます。座標は、参照システムとグリッドの概念と密接に関連しています。ほとんどの場合、文字と数字の組み合わせ。

半径ベクトル

タイトルから、すでに彼がそれ自体です。それにもかかわらず、我々はこれについてより詳細に議論する。ある点がある軌道に沿って移動し、1つまたは別の参照系の起点を正確に知っていれば、いつでも半径ベクトルを描くことができます。ポイントの初期位置を瞬時ポイントまたは最終ポイントに接続します。

軌道

これは、特定の参照フレーム内の重要な点の動きの結果として配置される連続線と呼ばれます。

速度（直線と角度の両方）

これは、身体がどれくらい速くこの距離間隔を通過するかを示す値です。

加速度（角度と直線の両方）

どのような法律とどのくらい速く、体の速度パラメータが変化しているかを示します。

おそらく、ここにあるのは - キネマティクスの基本要素重要なポイント。速度と加速度の両方がベクトル量であることに留意すべきである。そして、これは、彼らが単に示唆的な価値を持っているだけでなく、特定の方向性を持っていることを意味します。ところで、彼らは一方向と反対の両方に向けることができます。最初のケースでは、車体が加速し、2番目のブレーキが掛かります。

最も簡単なタスク

マテリアルポイントのキネマティクス（速度、加速と距離は実質的に基本的な概念である）は、膨大な数のタスクには及ばないが、それらの様々なカテゴリの多くには及んでいない。身体が移動する距離を決定するために、かなり簡単な問題を解決しようとしましょう。

私たちが手に持つ条件は、以下のとおりです。ライダーの車がスタートラインに立っています。オペレーターは旗を掲げて信号を発し、その場所から急に車が離れる。距離が100メートルに等しい場合、レーサーの競技で新しい記録を設定することができるかどうかを決定する、次のリーダーは7.8秒で合格した。車を加速させて3メートルに等しく、秒で四角に分けます。

だから、どのようにこの問題を解決するには？ 我々は特定のパラメータの「乾いた」定義を必要としないので、かなり面白いです。それはターンとある状況で明るくなり、指標の解決と探索のプロセスを多様化させます。しかし、我々がその課題に近づく前に、何を導くべきでしょうか？

1.重要ポイントのキネマティクスには、この場合の加速の使用が含まれます。

2.数値は条件に現れるため、距離式を用いて解を提案する。

問題は簡単に解決されます。 これを行うために、我々は距離式S = VoT +（ - ）AT ^ 2/2をとる。意味は何ですか？ライダーが指定された距離をどのくらい経過するかを調べ、スコアをレコードと比較して、彼が彼を倒すかどうかを調べる必要があります。この目的のために、時間を選択すると、AT ^ 2 + 2VoT - 2Sという式が得られます。これは二次方程式にすぎません。しかし、車は壊れてしまいます。つまり、初期速度は0になります。方程式を解くと、判別式は2400になります。時間を見つけるには、根を抽出する必要があります。小数点第2位を補う：48,98。方程式の根を見つけましょう：48.98 / 6 = 8.16秒。ライダーは既存の記録を破ることができないことが判明しました。